Solution:
in an isosceles triangle, the angles opposite of the apex are equal. The three angles in any triangle equal 180 degrees. Now, if we let x represent one of the angles opposite the apex, then the angel at the apex will be

Adding up the three angles will equal 180:

this is equivalent to:

that is:
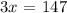
solving for x, we get:
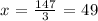
We can conclude that the angles in the isosceles triangle are 49 degrees, 49 degrees, and (x+33)= (49+33) = 82 degrees. Then, the correct answer is:
Angle 1: 49 degrees
Angle 2: 49 degrees
Angle 3: 82 degrees