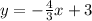For lines to be perpendicular, the slope of one of them must be the inverse negative of the other one. So for example given the lines:

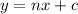
For them to be perpendicular their slopes must be:

To determine the equation of a line perpendicular to the given one, the first step is to calculate the slope of the graphed line.
Using two points of the line, for example: (0,3) and (4,6)
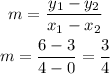
The slope of the graphed line is
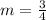
Now the slope of the perpendicular line must be the inverse negative so that:
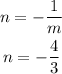
Now that we know the slope of the perpendicular line, and is given that it crosses the point (3,-1) we can use the point slope form to determine its equation

For our line
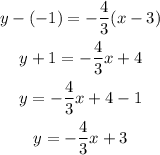
The equation of a perpendicular line of the one shown in the graph rthat goes through point (3,-1) is