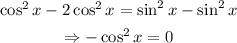ANSWER
Step-by-step explanation
We want to find the solution to the equation:
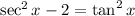
First, let us rewrite the trigonometric terms:
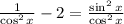
Multiply both sides of the equation by cos²x:
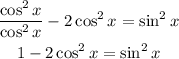
We have that:
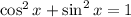
Substitute that for 1 in the equation:
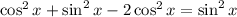
Simplify the equation above: