Question

Which linear inequality is represented by the graph?Y ≤ 2x + 4Y ≤ 1/2x+3Y ≥ 1/2x+3Y≥ 2x + 3

Answer 1

B

Step-by-step explanation:

First, we determine the equation of the line in the slope-intercept form: y=mx+b

From the graph:

• The y-intercept of the line, b = 3

Next, we determine the slope using any two points on the line.

We pick points (0,3) and (-2,2)

`\text{Slope }=(2-3)/(-2-0)=(-1)/(-2)=(1)/(2)`

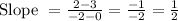
Therefore, the equation of the line of symmetry will be:

`y=(1)/(2)x+3`

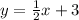
Next, we determine the inequality sign.

We use the origin(0,0) to test the required region.

`\begin{gathered} \text{When x=0 and y=0} \\ y=(1)/(2)x+3 \\ 0\boxed{\square}3 \\ \end{gathered}`

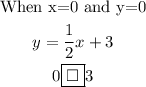
Since 0 is less than 3, the inequality sign will be less than or equal to.

Note: We use less than or equal to because we have a thick line.

We therefore have:

`y\leqslant(1)/(2)x+3`

The correct option is B.