To solve this problem we need the definition of like terms:
• Two terms will be called ",like terms," if they have the same variable or variables.
In this case, the expression we have is:
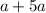
The first term is "a", it contains only the variable a.
The second term is "5a" it contains the coefficient 5 and the variable a.
Since the two terms have the same variable, the terms are like terms.
Answer: Yes