Given data
*The given initial velocity is u = 5.5 m/s
*The given total time is T = 3.7 s
*The value of the acceleration due to gravity is g = -9.8 m/s^2
The formula for the time taken by the gourd to reach the highest point of the cliff is given by the equatin of motion as
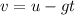
Here v = 0 m/s is the final velocity of the gourd at the highest point of the cliff
Substitute the known values in the above expression as
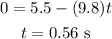
The height of the cliff is calculated by the equation of motion as
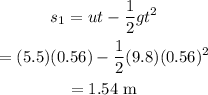
Hence, the height of the cliff is s_1 = 1.54 m
The time taken by the gourd to reach the peak height is calculated as
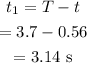
The formula for the peak height is given by the equation of motion as
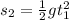
Substitute the known values in the above expression as
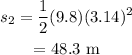
Hence, the peak height is s_2 = 48.3 m
The formula for the velocity of the gourd strikes into the ground below is given as
![v=\sqrt[]{2gs_2}](https://img.qammunity.org/2023/formulas/physics/college/bsx8tnkkaywgoq5ey4q2z4ihuli1mmna9b.png)
Substitute the known values in the above expression asv=
![\begin{gathered} v=\sqrt[]{2*9.8*48.3} \\ =30.76\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/1l5g6a9n3ltb3ldpjkhixsr5puj9s3ulf8.png)
Hence, the velocity of the gourd smash into the ground is v = 30.76 m/s