Question

In June she used 250 minutes and the cost was $80.00. In July she used 930 minutes and the cost was $216.00.

Answer 1

a)

We know that Jane's plan has a monthly fee and a charge per minute of calling time, this means that the cost can be express as a linear function where x is the number of minutes of calling time. Then we have a function of the form:

`C(x)=mx+b`

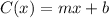
where m is the slope of the model and b is the y-intercept. In this case the slope will represent the charge per minute and b will represent the monthly fee. Now, to determine m and b we need to use the information given; we know that in June she used 250 minutes and the cost was $80, then we have the equation:

`250m+b=80`

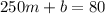
We also know that, on July, she used 930 minutes and she paid 216, then we have the equation:

`930m+b=216`

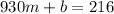
Hence, we have the system of equations:

`\begin{gathered} 250m+b=80 \\ 930m+b=216 \end{gathered}`

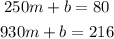
To find the solutions of the system, which will lead to the values of m and b, we solve the first equation for b:

`b=80-250m`

and plug this value on the second equation:

`\begin{gathered} 930m+80-250m=216 \\ 680m=216-80 \\ 680m=136 \\ m=(136)/(680) \\ m=0.2 \end{gathered}`

Once we know the value of m, we plug it in the equation we found for b:

`\begin{gathered} b=80-250(0.2) \\ b=80-50 \\ b=30 \end{gathered}`

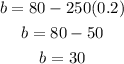
Now that we have the values of m and b we plug them in the cost function expression. Therefore, the cost function is:

`C(x)=0.2x+30`

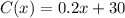
Note: This cost function tells us that the monthly fee of Jane's plan is $30 and the charge per minute is $0.20

b)

Now that we know the cost function for any number of minutes x we can plug any value to find the cost; in this case we want to know how much is the bill if she used 474 minutes, then x=474. Plugging this value of x we have:

`\begin{gathered} C(474)=(0.2)(474)+30 \\ C(474)=124.8 \end{gathered}`

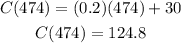
Therefore, the bill for August is $124.80