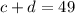Question

on a number line A is at 11, B is at 38, C is at c and D is at d. Points C and D trisect segment AB. what is the value of c+d?

Answer 1

First, find the positions of C and D. Draw a diagram to visualize the problem:

To find c and d, divide the distance between A and B over 3. Then, add the result to the position of A to find c, and then add again that number to the position of c to find d.

The distance between A and B equals the difference of their coordinates:

`d(A,B)=38-11=27`

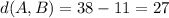
Divide 27 over 3:

`(27)/(3)=9`

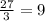
Add 9 plus 11 to find c:

`\begin{gathered} c=9+11 \\ =20 \end{gathered}`

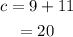
Add 9 plus 20 to find d:

`\begin{gathered} d=20+9 \\ =29 \end{gathered}`

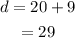
Since c=20 and d=29, then:

`c+d=20+29=49`

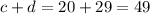
Therefore:

`c+d=49`