To answer this question, we can draw a rectangle to visualize it better:
As we can see, to answer this, we can use the Pythagorean Theorem, since the figure is a rectangle, and the inner angles of a rectangle are right angles (90 degrees). The players will need to run from one of the corners to the other diagonally across the field.
The Pythagorean Theorem says to us that: the square of the length of the hypotenuse is equal to the square of the length of one side plus the square of the length of the other side (this is applied only to right triangles). Then, we have that we need to find the length of the hypotenuse in the figure. Thus, we have:

And, now, we have:
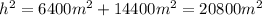
We need to take the square root to both sides of the equation:
![\sqrt[]{h^2}=\sqrt[]{20800m^2}\Rightarrow h=\sqrt[]{20800m^2}\Rightarrow h=144.22m](https://img.qammunity.org/2023/formulas/mathematics/college/qlikyrgac4cumxprct2rwk5k9fr150zlko.png)
Hence, the players will run, approximately, 144.22m (rounded to the hundredths.)