Answer
a) The statement is true.
"the formula for area of a sector is (degrees/360) area of circle.
b) Ratio = (1/6)
c) Area of the circle = 64π square units
d) Area of the sector = (64π/6) square units = (32π/3) square units
Step-by-step explanation
a) The area of a sector is a fraction of the area of a circle. This fraction presents that the sector is a small part of the circle. So,
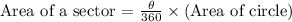
where θ is the angle subtended at the center of the circle by the arc.
So, this statement is true.
b) The ratio used to find the area of the sector is that of how to know what fraction of the circle is the sector.
Ratio = (θ/360°)
θ is the angle subtended at the center of the circle by the arc, measured in degrees.
For this question,
θ = 60°
Ratio = (θ/360°) = (60°/360°) = (1/6)
c) Area of a circle is given as
Area of a circle = πr²
where
π = pi
r = radius of the circle = 8
Area of the circle = πr²
Area of the circle = π (8²) = 64π square units
d) Area of the sector is given as
Area of the sector = (Ratio) × (Area of the circle)
Ratio = (1/6)
Area of the circle = 64π square units
Area of the sector = (Ratio) × (Area of the circle)
Area of the sector = (1/6) × (64π) = (64π/6) = (32π/3) square units
Hope this Helps!!!