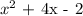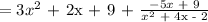Question

What is the result when 3x4 + 14x3 + 11x2 + 27x 9 is divided byx² + 4x – 2? If there is a remainder, express the result in the form q(x) +r(x)/b(s)

Answer 1

First use long division

STEPS:

Use first term of the divisor to divide the first term of the dividend,

then use the result to multiple all the terms in the divisor and subtract from the dividend.

repeat the same method till the degree of dividend is less than that of divisor

`\begin{gathered} \\ \text{ Quetient 3x}^2+2x\text{ + 9} \\ =x^2\text{ + 4x - 2}\sqrt[]{3x^4+14x^3+11x^2\text{ + 27x - 9}} \\ \text{ - 3x}^4+12x^3\text{ - 6}x^2 \\ \text{ 2x}^3+17x^2+27x\text{ - 9} \\ \text{ - 2x}^3+8x^2\text{ - 4x} \\ \text{ 9x}^2\text{ + 31x - 9} \\ \text{ - 9x}^2\text{ + 36x - 18} \\ \text{ Remainder -5x + 9} \\ \end{gathered}`

q(x) + r(x)/b(x)

q(x) is the quetient

`3x^2\text{ + 2x + 9}`

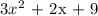
r(x) is the remainder

= -5x + 9

b(x ) is the divisor

`x^2\text{ + 4x - 2}`
`=3x^2\text{ + 2x + 9 + }\frac{-5x\text{ + 9}}{x^2\text{ + 4x - 2}}`