Question

The surface of a table to be built will be in the shape shown below. The distance from the center of the shape to the center of each side is 8.7 inches and the length of each side is 10 inchesAFс8.7 in.E10 in. DPart A: Describe how you can docompose this shape into triangles (2 points)Part B: What would be the area of each triangle? Show every step of your work. (5 points)Part C: Using your answers above, determine the area of the table's surface. Show every step of your work. (3 points)

Answer 1

Part A: You can descompose the given figure into six triangles by linking the opposite vertices with a line, as follow:

Part B: As the distance from the center of the shape to the center of each side is 8.7 inches and the length of each side is 10 inches, all the triangles have the same mesures and then the same area.

To find the area of a triangle you use the next formula:

`A=(1)/(2)(b*h)`

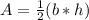
b is the base of the triangle (in this case it is 10in)

h is the height of the triangle (in this case it is 8.7in)

Then, the area of each triangle is:

`\begin{gathered} A=(1)/(2)(10in*8.7in) \\ \\ A=(87)/(2)in^2 \\ \\ A=43.5in^2 \end{gathered}`

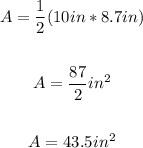
The area of each triangle is 43.5 sq.in.

Part C: As you divide the figure into 6 equal triangles (Part A) and each triangle has an area of 43.5 sq.in (Part B); multiply the area of each triangle by 6 to find the surface area of the table:

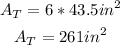
`\begin{gathered} A_T=6*43.5in^2 \\ A_T=261in^2 \end{gathered}`Then, the surface are of the table is 261 square inches