Lets solve the following example
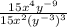
We can note that y is raised to the negative power of -9. Then, by the inverse law of exponents, we have
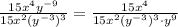
because
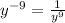
Now, we can see that

where we used the division rule of exponents, then our last result can be written as
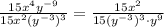
Now, by the power to a power rule, we can see that
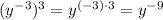
then, our last result can be written as
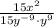
But
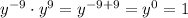
Then, the last result can be written as
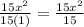
Finally, since 15 divided by 15 is one, we get
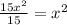
Therefore,
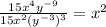
and we used the 3 properties.