Question

Can you please help me with 28 Please give all forms of the end behavior such as limits and as_,_

Answer 1

Let's analyze the function:

`f(x)=(x^2-4x+3)/(x^2-4x-5)`

To do this let's first find the domain of the function, since this is a rational function we know that the denominator can be zero so let's find for which values of x this happens:

`\begin{gathered} x^2-4x-5=0 \\ (x-5)(x+1)=0 \\ \text{then} \\ x-5=0 \\ x=5 \\ \text{ or} \\ x+1=0 \\ x=-1 \end{gathered}`

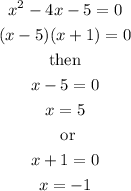
Hence we conclude that the fucntion is not defined for x=5 or x=-1, which means that the domain of the function is:

`\text{domain}f=(-\infty,-1)\cup(-1,5)\cup(5,\infty)`

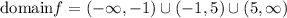
This also means that we may have somo vertical asympotes at x=5 and x=-1; to determine if we do we need to calculate the one-sided limits at those points if the result is negative or positive infinity we have vertical asymptotes. Let's calculate this limits:

`\lim _(x\to-1^-)(x^2-4x+3)/(x^2-4x-5)=\infty`

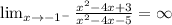
and

`\lim _(x\to5^-)(x^2-4x+3)/(x^2-4x-5)=-\infty`

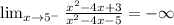
To determine this limits we notice that, as we approach both values the denominator increases arbitrarily when they approach the number from the left; for example, notice that:

`f(-1.0001)=((-1.0001)^2-4(-1.0001)+3)/((-1.0001)^2-4(-1.0001)-5)=13410.98`

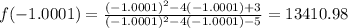
as we approach more an more to -1 the function value will increase and for that reason we conclude the results of the limits are what we stated.

Now, let's determine the zeros of the function:

`\begin{gathered} f(x)=0 \\ (x^2-4x+3)/(x^2-4x-5)=0 \\ x^2-4x+3=0 \\ (x-3)(x-1)=0 \\ \text{then } \\ x-3=0 \\ x=3 \\ \text{ or} \\ x-1=0 \\ x=1 \end{gathered}`

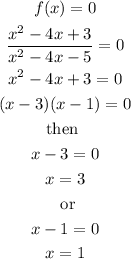
Hence the function is zero at x=3 and x=1.

Therefore, we conclude that the local behavior of the functions is:

• The function has two vertical asymptotes: x=-1 and x=5

,

• The zeros of the function are x=3 and x=1.

Now, let's find the end behavior. To do this we calculate the limits:

`\begin{gathered} \lim _(x\to-\infty)(x^2-4x+3)/(x^2-4x-5) \\ \text{and} \\ \lim _(x\to\infty)(x^2-4x+3)/(x^2-4x-5) \end{gathered}`

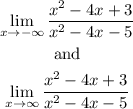
Let's find the first one:

`\begin{gathered} \lim _(x\to-\infty)(x^2-4x+3)/(x^2-4x-5)=\lim _(x\to-\infty)((x^2)/(x^2)-(4x)/(x^2)+(3)/(x^2))/((x^2)/(x^2)-(4x)/(x^2)-(5)/(x^2)) \\ =\lim _(x\to-\infty)(1-(4)/(x)+(3)/(x^2))/(1-(4)/(x)-(5)/(x^2)) \\ =(1)/(1) \\ =1 \end{gathered}`

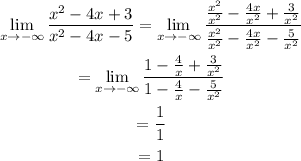
And:

`\begin{gathered} \lim _(x\to\infty)(x^2-4x+3)/(x^2-4x-5)=\lim _(x\to\infty)((x^2)/(x^2)-(4x)/(x^2)+(3)/(x^2))/((x^2)/(x^2)-(4x)/(x^2)-(5)/(x^2)) \\ =\lim _(x\to\infty)(1-(4)/(x)+(3)/(x^2))/(1-(4)/(x)-(5)/(x^2)) \\ =(1)/(1) \\ =1 \end{gathered}`

Since both limits are the same we can conclude that we only have one horizontal asymptote, and that it's given as:

`y=1`

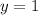
Therefore, the horizontal asymptote is y=1 and this described the end behaviour of the function that can be also written as:

`\begin{gathered} \text{ As }x\rightarrow\infty,f(x)\rightarrow1 \\ \text{ As }x\rightarrow-\infty,f(x)\rightarrow1 \end{gathered}`

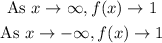
All the information we found can be seen in the graph of the function: