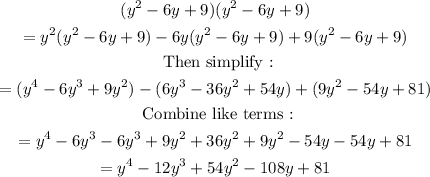ANSWER :
The answer is A. y^4 - 12y^3 + 54y^2 - 108y + 81
EXPLANATION :
From the problem, we have the expression :
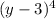
we can write it as :
![(y-3)^4=[(y-3)^2]^2](https://img.qammunity.org/2023/formulas/mathematics/college/ikr6x220yucbtnm9gd3lrl0x7ffqsgcb03.png)
Perform the first power to the 2nd using :
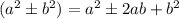
![[(y-3)^2]^2=(y^2-6y+9)^2](https://img.qammunity.org/2023/formulas/mathematics/college/ivs4o4vj5oeczfixyedc5sxeqqz1g6syn6.png)
Next is to perform the next square :

We can distribute each term of the first parenthesis to the second parenthesis as :
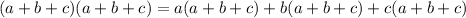
Then :