Answer:
(a) 6.91 m/s
(b) -0.52 m/s²
Step-by-step explanation:
Part (a)
To find the truck's original speed, we will use the following equation
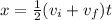
Where x is the distance covered, vi is the initial speed, vf is the final speed, and t is the time. Solving for vi, we get:
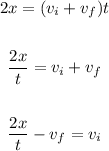
Now, we can replace x = 40.0 m, t = 8.55s and vf = 2.45 m/s, so
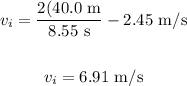
Part (b)
Now, we can calculate the acceleration using the following equation:
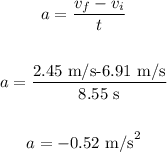
Therefore, the answers are
(a) 6.91 m/s
(b) -0.52 m/s²