Given
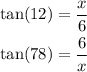
To check whether the value of x is found using both equation:
It is known that,
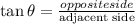
From the given figure, it is clear that the angles of the triangle ABC,

Therefore for the angle C=12 degree,
The equation can be written as,
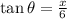
Since x is the opposite side and 6 is the adjacent side.
However for angle B. the opposite side will be 6 and the adjacent side will be x.
Thus, we get

Hence, Andre and Mia both are correct.