Question

A sample of a gas is occupying a 450 mL container at a pressure of 167 kPa and a temperature of 295 K. If the pressure is increased to 230 kPa and the volume is decreased to 400 mL, what is the new temperature in K?

Answer 1

Answer: the new temperature of the sample of gas is 361 K

Step-by-step explanation:

The question requires us to determine the new temperature of a sample of gas, knowing that its pressure was increased and volume decreased.

The following information was provided by the question:

initial volume = V1 = 450 mL

initial pressure = P1 = 167 kPa

initial temperature = T1 = 295 K

final volume = V2 = 400 mL

final pressure = P2 = 230 kPa

Assuming that this gas behaves as an ideal gas, we can apply the equation of ideal gases:

`PV=nRT`

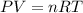
where P corresponds to the pressure of the gas, V is the volume of the gas, n corresponds to the number of moles of gas, R is the gas constant and T is the temperature of the gas.

Note that, even though the pressure, volume and temperature of a sample of gas changes, the number of moles of gas contained in this sample (n) does not change. Thus, with the information of initial volume, pressure and temperature, we can find an expression for the number of moles of gas and then use it to calculate the final temperature of the gas.

In summary, we'll follow these steps:

1) rearrange the equation of ideal gases to determine n;

2) use the values provided by the question to find a mathematical expression for n;

3) rearrange the equation of ideal gases to determine T;

4) use the values of final pressure and volume, provided by the question, and the expression of n determined in the previous step to calculate the new temperature of the gas.

First, let's rewrite the equation of gas in a way we can calculate the number of moles:

`PV=nRT\rightarrow n=(PV)/(RT)`

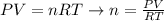
Next, let's use the values of initial pressure (P1), initial volume (V1) and initial temperature (T1) to write a mathematical expression for n:

`n=(P_1V_1)/(RT_1)\rightarrow n=((167kPa)*(450mL))/(R*(295K))=(255)/(R)(kPa.mL)/(K)`

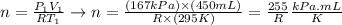
(note that the gas constant, R, as well as the units were kept in the expression - that is because we~ll replace the entire expression into the equation to calculate the temperature).

Next, we'll need to rearrange the equation of ideal gases in order to find an expression to calculate the temperature:

`PV=nRT\rightarrow T=(PV)/(nR)`

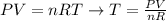
And at last, we'll use the values of final pressure (P2) and final volume (V2) provided by the question, as well as the expression for n determined above, to calculate the final temperature of the sample of gas:

`T_2=(P_2V_2)/(nR)\rightarrow T_2=((230kPa)*(400mL))/(((255)/(R)(kPa.mL)/(K))* R)=361K`

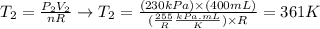
Therefore, the new temperature of the sample of gas is 361 K.