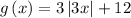Question

Let g (x) be the indicted transformation of f (x) = - I3xl -4. Stretch the graph of f (x) = - l3xl - 4 vertically by a factor of 3 and reflect it across the x-axis. Identify the rule and graph of g (x).

Answer 1

we have the parent function f(x)

`f\left(x\right)=-\left|3x\right|-4`

step 1

Stretch the graph of f (x) vertically by a factor of 3

The rule is given by

(x,y) --------> (x,3y)

so

`-\left|3x\right|-4----->\text{ }-3\left|3x\right|-12`

step 2

Reflection across the x-axis

The rule is given by

(x,y) -------> (x,-y)

so

`-3\left|3x\right|-12\text{ -----> }3\lvert3x\rvert+12`

therefore

The function g(x) is

`g\left(x\right)=3\left|3x\right|+12`