Consider that the maximum wire-feed speed is 350 mm/sec,
![S_(\max )=350\text{ }\frac{\operatorname{mm}}{\sec }]()
Its is asked to convert the expression into inches per minute.
Consider the following conversions,
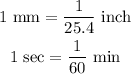
Then, it follows that,
![\begin{gathered} 1\text{ }\frac{\operatorname{mm}}{\sec }=\frac{((1)/(25.4))\text{ inch}}{((1)/(60))\text{ min}} \\ 1\text{ }\frac{\operatorname{mm}}{\sec}=(1)/(25.4)*(60)/(1)\frac{\text{ inch}}{\text{ min}} \\ 1\text{ }\frac{\operatorname{mm}}{\sec}\approx2.3622\frac{\text{ inch}}{\text{ min}} \end{gathered}]()
Substitute this conversion of units in the expression for speed,
![\begin{gathered} S_(\max )=350\text{ }\frac{\operatorname{mm}}{\sec } \\ S_(\max )=350\text{ }\cdot\text{(1 }\frac{\operatorname{mm}}{\sec}) \\ S_(\max )=350\cdot(2.3622\text{ }\frac{\text{ inch}}{\min }) \\ S_(\max )\approx826.77\text{ }\frac{\text{ inch}}{\min} \end{gathered}]()
Thus, the maximum speed is equivalent to 826.77 inches per minute.