Question

Aline intersects the points (-22, -14) and(-18, -12). What is the slope-interceptequation for this line?y =ExX +Simplify the fraction completely.

Answer 1

To answer this question, we need to find the slope of the line, and then, we can use the Point-Slope Form of the line, to finally find the Slope-Intercept equation of the given line.

1. Finding the Slope of the line

To find it, we need to apply the formula:

`m=(y_2-y_1)/(x_2-x_1)`

We have that the points are:

(-22, -14) and (-18, -12)

We can label these points as:

(-22, -14) ---> x1 = -22, y1 = -14

(-18, -12) ---> x2 = -18, y2 = -12

Then, applying the formula for the slope of a line, we have:

`m=(y_2-y_1)/(x_2-x_1)=(-12-(-14))/(-18-(-22))=(-12+14)/(-18+22)=(2)/(4)=(1)/(2)\Rightarrow m=(1)/(2)`

2. Finding the Point-Slope Form of the line (first)

The associated formula is given by:

`y-y_1=m(x-x_1)`

We can take any of the points above. Let us select (-22, -14). Then, we have:

`y-(-14)=(1)/(2)\cdot(x-(-22))\Rightarrow y+14=(1)/(2)\cdot(x+22)`

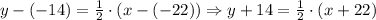
Then, expanding and simplifying this partial result:

`y+14=(1)/(2)x+(1)/(2)\cdot22\Rightarrow y+14=(1)/(2)x+11`

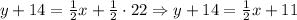
Now, subtracting 14 to both sides of the equation:

`y+14-14=(1)/(2)x+11-14\Rightarrow y=(1)/(2)x-3`

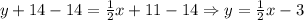
We already have the Slope-Intercept equation of the line, since the formula for this is as