Question

All you need is in the photo PLEASE ANSWER FAST

Answer 1

We will investigate the use of Venn diagrams to determine the respective probabilities.

A Algebra 2 class consists of total students ( T ):

`T\text{ = 29 students}`

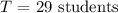
We will define two sports events ( A ) and ( B ) as follows:

`\begin{gathered} A\text{ : Students who play basketball} \\ B\text{ : Students who play baseball} \end{gathered}`

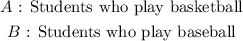
We will define the respective proportions of students associated with each event using set notations.

`\begin{gathered} A\text{ = 17 , B = 6} \\ p(A)=(17)/(29)\text{ , p ( B ) = }(6)/(29) \end{gathered}`
`A^(\prime)\text{ \& B' = 8 students}`
`p\text{ ( A' \& B' ) = }(8)/(29)`

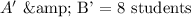
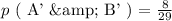
We will construct a venn Diagram to grasp the entire distribution of events in the Algebra class:

From the above venn diagram and using the law of probabilities i.e all probabilities concerning a universal set must add up to 1.

`\text{Sum of all probabilities = 1}`
`p\text{ ( A ) + p ( B ) - p ( A \& B ) + p ( A' \& B' ) = 1}`

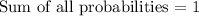
We will use the above universal law of probabilities to determine the probability that a randomly chosen student from the class plays both basketball and baseball ( A & B ):

`\begin{gathered} (17)/(29)\text{ + }(6)/(29)\text{ + }(8)/(29)\text{ - 1 = p ( A \& B )} \\ \\ \text{p ( A \& B ) = }(31)/(29)\text{ - 1} \\ \\ \text{p ( A \& B ) = }\frac{31\text{ - 29}}{29}\text{ = }(2)/(29) \\ \\ \text{p ( A \& B ) = }(2)/(29)\text{ = 0.069 }\ldots\text{ Answer} \end{gathered}`