Question

Which function matches the graph?A. f(x) = (x-4)³(x + 2)B. f(x) =(x + 4)³(x - 2)C. f(x) = (x + 4)(x - 2)³2D. f(x) = (x4) (x + 2)³E. f(x) = (x+4)³(x - 2)³

Answer 1

The roots of the graph are -4 and 2. This means that the factors of the graph will be:

`(x+4)\text{ and }(x-2)`

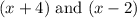
Notice the way the graph behaves at x = -4. We can see that while the graph cuts the x-intercept at that point, it kind of rests on the line. This means that the multiplicity of the root is odd, but not 1.

The behavior at x = 2 is just a normal intersection of the x-axis, so the multiplicity will be 1.

Therefore, we can assume that the function of the graph will be:

`f(x)=(x+4)^3(x-2)`

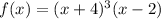
OPTION B is the correct option.