Question

In the function, the slope will be multiplied by 1/2, and the y-value of the y-intercept will be increased by 3 units. Which of the following graphs best represents the new function?

Answer 1

Option Y is correct.

Step-by-step explanation

We are told that the slope is multiplied by (1/2) and the y-intercept is increased by 3 units.

The original graph has a y-intercept (point where the graph crosses the y-axis) at point y = 1. Adding 3 units to that, changes the y-intercept to y = 4.

And that leaves options X and Y as viable answers.

But the original graph is positive sloping, and multiplying the slope by (1/2) only spreads the graph out more along the y-axis, it doesn't change the direction of the graph like option X has been changed to be negative sloping. This would only happen if the slope was multiplied by a negative number.

So, this leaves us with only Option Y as the viable answer.

And to be absolutely sure, we can go further and calculate the slope of the original graph and the graph in option Y.

For a straight line, the slope of the line can be obtained when the coordinates of two points on the line are known. If the coordinates are (x₁, y₁) and (x₂, y₂), the slope is given as

`Slope=m=\frac{Change\text{ in y}}{Change\text{ in x}}=(y_2-y_1)/(x_2-x_1)`

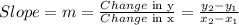
For the original question,

(x₁, y₁) and (x₂, y₂) are (0, 1) and (-1, -1)

`\text{Slope = }(-1-1)/(-1-0)=(-2)/(-1)=2`

For the option Y,

(x₁, y₁) and (x₂, y₂) are (0, 4) and (-1, 3)

`\text{Slope = }(3-4)/(-1-0)=(-1)/(-1)=1`

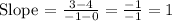
1 is indeed half of 2. This confrims our answer.

Hope this Helps!!!