Question

The magnetic filed of 17.5 mT exists inside a solenoid of length 12.0 cm when the electric current of 250. mA flows in the coil. How many turns the solenoid has?

Answer 1

Given data:

* The magnetic field inside the solenoid is,

`\begin{gathered} B=17.5\text{ mT} \\ B=17.5*10^(-3)\text{ T} \end{gathered}`

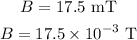
* The length of the solenoid is,

`\begin{gathered} l=12\text{ cm} \\ l=12*10^(-2)\text{ m} \end{gathered}`

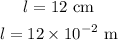
* The current through the solenoid is,

`\begin{gathered} I=250\text{ mA} \\ I=250*10^(-3)\text{ A} \end{gathered}`

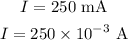
Solution:

The magnetic field inside the solenoid is,

`B=\mu_oNI`

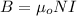
where N is the number of turns in the solenoid,

`\mu_o\text{ is the permeability of free space}`

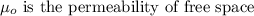
Substituting the known values,

`\begin{gathered} 17.5*10^(-3)=4\pi*10^(-7)* N*250*10^(-3) \\ 17.5*10^(-3)=3141.59*10^(-10)* N \\ N=(17.5*10^(-3))/(3141.59*10^(-10)) \\ N=0.00557042*10^(-3+10) \\ N=0.00557042*10^7 \\ N=55.7042*10^3 \\ N=55704.2 \\ N\approx55704 \end{gathered}`

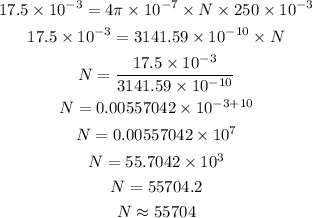
Thus, the number of turns in the solenoid is 55704.