The given quadratic equation is;
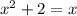
This can be written properly as;
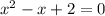
The discriminant is used to test for nature of roots of a quadratic equation and it is given by the equation;
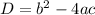
From the given quadratic equation;
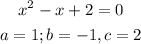
Thus, the discriminant will be;
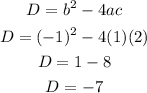
Since the discrimiant has a value(-7) less than zero(0), thus it has two(2) complex roots.
Hence, the correct option is option B