Question

Determine if the following equation has x-axis symmetry, y-axis symmetry, origin symmetry, or none of these.

Answer 1

we need to solve this graphically first and then test for x-axis symmentry

to test for x-axis symmentry, replace y with (-y) and simplify the equation.

if the equation is equivalent to the original equation, then the graph is symmentrical to x-axis

`-(2)/(x)=y+2_{}`

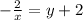
now let's test for (-y) and compare

`-(2)/(x)=-y+2`

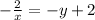
since the resulting equation is not similar to the original equation, the equation is not symmentrical to the x-axis.

now let's test y axis

replace x with (-x)

`\begin{gathered} -(2)/(x)=y+2 \\ -(2)/((-x))=y+2 \\ (2)/(x)=y+2 \end{gathered}`

the equation is not symmentrical to the y-axis

from the calculation above, the equation is not symmentrical to both x and y axis.