Question

The type and number of fish caught in the Charleston Harbor in March was recorded for a month. The results are recorded in the table below. What is the probability that the next fish caught is a Drum or Bluefish? Enter a fraction or round your answer to 4 decimal places, if necessary. Flounder-289, Red Drum-367, Black Drum-161, Bluefish-295, Sea Trout-151

Answer 1

Given: The type and number of fish caught in the Charleston Harbor in March was recorded for a month

To Determine: The probability that the next fish caught is a Drum or Bluefish

Solution

Calculate the total number of fish caught

`\begin{gathered} Flounder=289 \\ Red-Drum=367 \\ Black-drum=161 \\ Blue-fish=295 \\ Sea-trout=151 \\ Total=1263 \end{gathered}`

It can be observed that we have two types of drum, red drum and black drum. The probability that the next fish caught is a drum or blue fish would be

Probability of red drum or black drum or blue fish

Note that

`\begin{gathered} P(A)=(n(A))/(n(S)) \\ P(A)=Probablity\text{ of A} \\ n(A)=Number\text{ of A} \\ n(S)=Number\text{ of total outcome} \\ P(A,OR,B)=P(A)+P(B) \end{gathered}`

Therefore, the probability hat the next fish caught is a drum or blue fish would be

`\begin{gathered} P(RD,OR,BD,OR,BF)=P(RD)+P(BD)+P(BF) \\ RD=Red-drum \\ BD=Black-drum \\ BF=Blue-fish \end{gathered}`

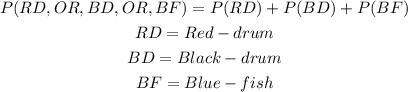
So,

`P(RD)+P(BD)+P(BF)=(367)/(1263)+(161)/(1263)+(295)/(1263)`
`\begin{gathered} =(367+161+295)/(1263) \\ =(823)/(1263) \end{gathered}`

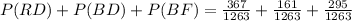
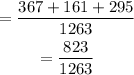
Hence, the probability hat the next fish caught is a drum or blue fish is 823/1263 or 0.6516