The rule for a rotation 90° clockwise about the origin is the following:
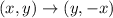
In this case, you can identify that the points A and B of the segment AB, are:
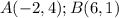
Applying the rule shown above, you can determine that the points A' and B' of the Image A'B' are:
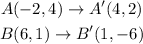
Now let's find the slopes of the segments AB and A'B' with the following formula:

Then:
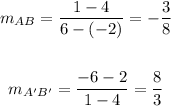
By definition, the slopes of perpendicular lines are opposite reciprocals. Therefore, you can conclude that the segments AB and A'B' are perpendiculars.
By definition, in rotation the lenghts do not change.
Knowing the above, you can conclude that, those segments are perpendicular and have equal lenght.
The answer is: Option (2)