Question

Nancy started the year with $425 in the bank and is saving $25 per week. Seamus started the year with $875 and is spending $15 per week. Write a system of equations representing this problem. Solve your system of equations to determine when they will have the same amount of money in the bank.

Answer 1

For the given problem let y = the bank saving, and x = number of weeks

Nancy started the year with $425 in the bank and is saving $25 per week.

So, we can write the following equation:

`y=25x+425`

Seamus started the year with $875 and is spending $15 per week.

So, we can write the following equation:

`y=-15x+875`

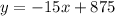
So, the system of equations will be as follows:

`\begin{gathered} y=25x+425\rightarrow(1) \\ y=-15x+875\rightarrow(2) \end{gathered}`

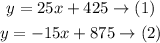
We will solve the system of equations by the substitution method

Substitute with (y) from equation (1) into equation (2)

So, we can write the following equation:

`25x+425=-15x+875`

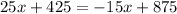
Solve for (x), combine the like terms:

`\begin{gathered} 25x+15x=875-425 \\ 40x=450 \\ x=(450)/(40)=11.25 \end{gathered}`

So, the answer will be:

They will have the same amount of money after 11.25 weeks.