Question

2. In the diagram below, B is the midpoint of AC and E is the midpoint of AD. If AB = 3, BE = 5, and AD=8what is the perimeter of BCDE?

Answer 1

Recall the Triangle Midsegment Theorem:

This implies that since BE is a midsegment of the triangle (as B and E are midpoints), then:

`BE=(1)/(2)CD`

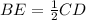
Substitute BE=5 into the equation and solve for CD:

`\begin{gathered} 5=(1)/(2)CD \\ \Rightarrow CD=5*2=10 \end{gathered}`

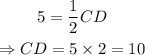
Since the point B is a midpoint, it follows by definition that:

`\begin{gathered} BC=AB,\text{ but AB=3} \\ \Rightarrow BC=3 \end{gathered}`

Also, E is a midpoint of AD, it follows that:

`\begin{gathered} ED=(1)/(2)AD \\ \Rightarrow ED=(1)/(2)*8=4 \end{gathered}`

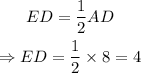
The perimeter of BCDE is the sum of all sides:

`P=BC+CD+ED+BE`

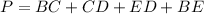
Substitute the length of the sides:

`P=3+10+4+5=22\text{ units}`

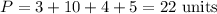
The perimeter of BCDE is 22 units.