Question

A graphics designer is designing an advertising brochure for an art show. Each page of the brochure is rectangular with an area of 30 in^2 and a perimeter of 22 in. Find the dimensions of the brochure.The longer side is nothing in.The shorter side is nothing in.

Answer 1

Recall that one page of the brochure would be a rectangle of the form

We are told that the area of this rectangle is 30 squared inches. For this rectangle, the area would be

`x\cdot y`

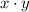
So we have the equation

`x\cdot y=30_{}`

Also, we are told that the perimeter of the figure is 22 in. Recall that the perimeter of the rectangle is obtained by adding the lengths of the sides of the figure. So we have the equation

`x+y+x+y=22=2x+2y`

Dividing both sides by 2, we get

`x+y=11_{}`

Using the first equation we have

`y=(30)/(x)`

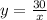
So if we replace this in the second equation, we have

`x+(30)/(x)=11`

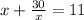
If we multipy both sides by x, we get

`x^2+30=11x_{}`

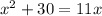
Subtracting 11x from both sides, we get

`x^2-11x+30=0`

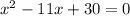
Recall that given an equation of the form

`ax^2+bx+c=0`

The solutions are given by the formula

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this case we have a=1, b= -11 and c=30

`x=\frac{-(-11)\pm\sqrt[]{(-11)^2-4\cdot1\cdot30}_{}}{2\cdot1}=\frac{11\pm\sqrt[]{121-120}}{2}=(11\pm1)/(2)`

From where we get

`x_1=(11+1)/(2)=(12)/(2)=6`

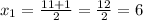
and

`x_2=(11-1)/(2)=(10)/(2)=5`

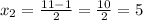
So, if x=6, we have that

`y=(30)/(6)=5`

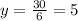
and if x=5, we have that

`y=(30)/(5)=6`

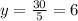
This means that the longer side is 6 inches long and the shorter side is 5 inches long