Question

The table shows the number of coins in a change dish. If Malcom selects two coins at random without replacement, what is the probability that he selects a nickel followed by a dome? Express your answer as a decimal rounded to the nearest thousandth

Answer 1

Given a table showing the number of 4 different coins

To Determine: Probability of selecting nickel, followed by dime, without replacement

Solution

The total of balls would be

`\begin{gathered} \text{Penny}=====8 \\ \text{Nickel}=====6 \\ \text{Dime}======8 \\ \text{Quarter}=====7 \\ \text{Total}=======29 \end{gathered}`

The probability of selecting nickel, followed by dime, without replacement is

`P(ND)=(6)/(29)*(8)/(28)`
`\begin{gathered} P(ND)=(48)/(812)=0.0591133 \\ \approx0.059(nearest\text{ thousandths}) \end{gathered}`

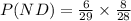
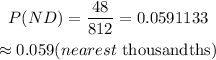
Hence, the probability of selecting nickel, followed by dime, without replacement expressed to the nearest thousandth is 0.059