Question

What are the missing numbers 1.4 1/[] x 1 5/7 =54/72.3 []/3 x 2 1/2 = 25/33.1 1/4 x [] 2/9 = 25/9

Answer 1

Part 1.

In this case, we have that

`(1)/(x)*1(5)/(7)=(54)/(7)`

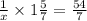
where x denotes the unknown number. Since the mixed number

`1(5)/(7)=(7\cdot1+5)/(7)=(12)/(7)`

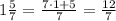
our equation can be writen as

`(1)/(x)*(12)/(7)=(54)/(7)`

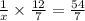
By multipliying both sides by 7, we have

`(1)/(x)*12=54`

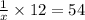
and by dividing both sides by 12, we get

`\begin{gathered} (1)/(x)=(54)/(12) \\ \text{then} \\ (1)/(x)=(27)/(6)=(9)/(2) \end{gathered}`

which means that

`x=(2)/(9)`

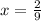
so, the missing number for the first question is 2/9

Part 2.

In this case, we have

`(x)/(3)*2(1)/(2)=(25)/(3)`

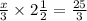
which can be rewriten as

`(x)/(3)*(5)/(2)=(25)/(3)`

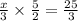
By multiplying by 3 both sides, we have

`x*(5)/(2)=25`

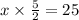
and by multiplying by 2 and dividing by 5 both sides, we get

`\begin{gathered} x=25*(2)/(5) \\ x=5*2 \\ x=10 \end{gathered}`

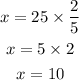
so the answer to the second question is 10

Part 3.

In this case, we have