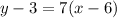Answer:
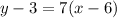
Explanation:
Pre-Solving
We are given that a line has a slope (m) of 7 and passes through the point (6,3).
We want to write the equation of this line.
There are three ways to do it:
- Slope-intercept form, which is y=mx+b where m is the slope and b is the value of y at the y-intercept.
- Point-slope form, which is
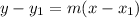 where m is the slope and
where m is the slope and
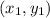 is a point.
is a point. - Standard form, which is ax+by=c where a, b, and c are free integer coefficients.
As the question doesn't specify, either form should work, but let's write the equation in point-slope form as that's the easiest to do.
Solving
As we are already given both the point and the slope, we can plug them both into the equation.
Starting with the slope, substitute 7 for m.
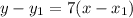
Now, substitute 6 as
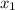 and 3 as
and 3 as
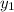 .
.