From the given table, let's determine if the table represents an exponential function.
An exponential function is a function that represents the relationship where a constant change in the indpenedent variable (x-values) given the same proortional change in the dependent variable (y-values).
An exponential function has the form:
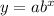
Let's check for the rate of change in the table is constant.
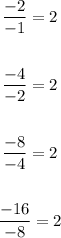
We can see the common ratio is 2.
The function is in the form:
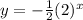
Therefore, we can say the table represents aan exponential function.
The common ratio is = 2.
This function represents an exponential decay function.
ANSWER:
Yes, it represents an exponential function.
Common ratio = 2
It represents an exponential decay function