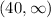Answer:
• The number of checks, c is greater than 40.
,
• (40, ∞)
Explanation:
Let the number of checks per month = c
Plan A
• Base service charge = $9.00 per month.
,
• Charge per check =7 cents = $0.07
The total cost for plan A is: 9+0.07c
Plan B
• Base service charge = $1.00 per month.
,
• Charge per check =27 cents = $0.27
The total cost for plan B is: 1+0.27c
For plan A to be better than plan B, the total cost for plan A must be less than the total cost for plan B. That is:

The inequality is solved for c.
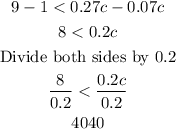
Plan A will be better than Plan B whenever the number of checks is greater than 40.
This can be written in the interval notation as: