Any number can be represented as:
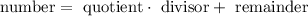
The quotient is the result of the division and the divisor is the number we are dividng for, the remainder is the pat that can't be divided. We have two unkown numbers divided by 16 we only know that one has the remainder of 11, while the other has the remainder of 14, so we can represent them as:
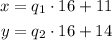
If we add these two numbers we can add the right side of the equation as well. Since the numbers are being divided by 16 we can represent the result as the individual quotients plus the remainder. If the remainder is greater than 16 we need to subtract 16 from the remainder and add 1 to the quotient.
a)
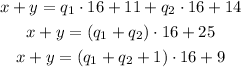
The remainder is 9.
Since the old divisor is divisible by the previous one we can divide them and multiply the quetiont by the result, that way we can represent the numbers with the new divisor (8). We have the remainder as 9 from the previous problem, but 9 is greater than 8, so we need to perform the same as before, we will subtract 8 from the remainder and add 1 to the quotient.
b) When we divide them by 8 we have:
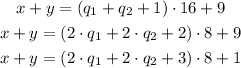
The remainder is 1.