Question

the mean clotting time of blood is 7.45 seconds with a standard deviation of 3.6 seconds. what is the probability that an individual's clotting time will be less than 6 seconds or greater than 9 seconds? assume A normal distribution. round to the nearest thousandth

Answer 1

We will investigate how to use a normally distributed population to determine the probability of occurunce of an event.

A population considers the clotting time of blood. We will define a random variable ( X ) as follows:

`X\colon\text{ The clotting of blood}`

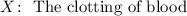
We are given that the random variable population follows a normal distribution with parameters:

`\begin{gathered} \text{Mean ( }\mu\text{ ) = 7.45} \\ \text{Standard deviation ( }\sigma\text{ ) = 3.6 } \end{gathered}`

The a normally distributed random variable X is described as:

`\begin{gathered} X\text{ \textasciitilde Norm ( }\mu\text{ , }\sigma^2) \\ X\text{ \textasciitilde{}Norm ( 7.45 , 3.6}^2) \end{gathered}`

We are to determine the probability of an event that occurs within the normally distributed population. An induvidual's blood clotting times is less than 6 seconds or greater than 9 seconds.

We can use the normal distribution bell curve to mark where these limiting points of an induvidual lie and the region that expresses the required probability.

To determine the required probability we will employ the standardizing equation as follows: