The perimeter of a figure is the length of its outer sides.
In this case, we need to find the perimeter of the semi-circle on the top and the highlighted sides of the two triangles at the bottom.
The perimeter of a semi-circle is given by the following formula:
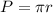
Where r is the radius of the semi-circle.
The length of the missing sides of the triangles is given by the Pythagorean theorem, like this:
![a=\sqrt[]{b^2^{}+c^2}](https://img.qammunity.org/2023/formulas/mathematics/college/zgi71g3itspyuejo1x5q3vttn4iu1grtpm.png)
Where b and c are the lengths of the legs of the triangles.
By replacing 8 for r into the first formula, we get:

By replacing 8 for b and 15 for c into the second equation, we get:
![a=\sqrt[]{8^2+15^2}=\sqrt[]{64+225}=\sqrt[]{289}=17](https://img.qammunity.org/2023/formulas/mathematics/college/wyd6cejy2vwry8a54y10xy83d5nhdz1kwe.png)
Then, we just have to add up the perimeter of the semi-circle and the lengths of the mentioned sides, two times, because there are two triangles, like this:
Perimeter = 8π + 17 + 17 = 8π + 34
Then, the perimeter of figure a equals 8π + 34 meters
The area of this figure can be calculated by summing up the area of the semicircle and the area of the triangle, like this:
The area of the semi-cirlce (red shaded area) is given by the following formula:
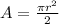
The area of the triangle (yellow shaded area) is given by the following formula:
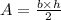
Where b is the length of the base and h is the height of the triangle.
By replacing 8 for r into the first formula, we get:
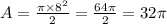
By replacing 15 for h and 16 for b ( 8 + 8) into the second formula, we get:
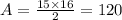
By adding the area of the semi-circle and the area of a triangle, we get:
Area = 32π + 120
Then, the area of the figure equals 32π + 120 square meters