Question

Solar panels installed in a backyard have a cross section that is a right triangle. The diagram shows the approximate dimensionsof this cross section. A vertical support from the right angle to the ground is recommended. Approximate the length of thesupport to the nearest tenth of a foot.

Answer 1

Option (A).

Given:

A right traingular backyard with dimensions is given as 13.6 ft, 4.4 ft and 14.3 ft.

The objective is to find the length of the vertical support .

Consider the required vertical component as y.

The diagram can be represented as,

Apply Pythagorean theorem to right triangle ADC.

`\begin{gathered} AC^2=AD^2+DC^2 \\ 13.6^2=(14.3-x)^2+y^2 \\ 13.6^2=14.3^2+x^2-2(14.3)(x)+y^2 \\ 184.96=204.49+x^2-28.6x+y^2 \\ x^2=184.96-204.49+28.6x-y^2 \\ x^2=-y^2-19.53+28.6x\ldots\ldots\ldots\ldots\ldots(1) \end{gathered}`

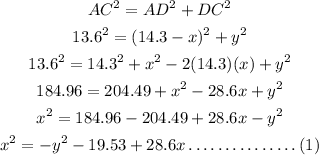
Now, apply Pythagoren theorem to right triangle CDB.

`\begin{gathered} CB^2=CD^2+DB^2 \\ \text{4}.4^2=y^2+x^2 \\ x^2=4.4^2-y^2 \\ x^2=19.36-y^2\ldots\ldots\ldots\ldots\ldots(2) \end{gathered}`

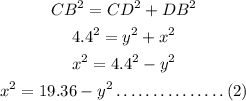
Equate equation (1) and (2).

`\begin{gathered} -y^2-19.53+28.6x=19.36-y^2 \\ -19.53+28.6x=19.36 \\ 28.6x=19.36+19.53 \\ 28.6x=38.89 \\ x=(38.89)/(28.6) \\ x\approx1.4 \end{gathered}`

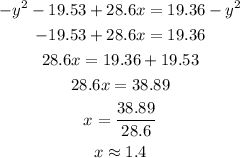
Let's susbtitue the value of x in equation (2) to find the value of y.

`\begin{gathered} 1..4^2=19.36-y^2 \\ 1.96=19.36-y^2 \\ -y^2=1.96-19.36 \\ -y^2=-17.4 \\ y=\sqrt[]{17.4} \\ y\approx4.2 \end{gathered}`

Thus, the distance of vertical component right triangle os 4.2 ft.

Hence, option (A) is the correct answer.