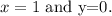Dividing the first equation by -3 we get:
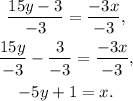
Substituting x=-5y+1 in the second equation we get:
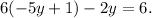
Applying the distributive property we get:
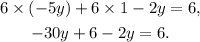
Adding like terms we get:
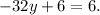
Subtracting 6 from the above equation we get:
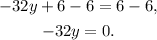
Dividing the above equation by -32 we get:
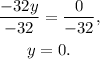
Finally, substituting y=0 in x=-5y+1 we get:
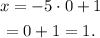
Answer: The solution to the given system of equations is: