Question

A dolphin dives down into the ocean and resurfaces along a path that is modeled by x2 – 8x + 4y = 0, where the distances are in feet. How many feet is the dolphin from its starting point along the water's surface?8 feet6 feet4 feet0 feet

Answer 1

the dolphin is 8 ft from its starting point (option A)

Step-by-step explanation:

The path model:

`x^2\text{ - 8x + 4y = 0}`

Considering the water's surface as the starting point, the value of y = 0

And x = distance from its starting point

We substitute for y in the model:

`\begin{gathered} x^2\text{ - 8x + 4(0) = 0} \\ x^2\text{ - 8x = 0} \end{gathered}`

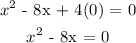
Then we find the values of x:

`\begin{gathered} x^2\text{ - 8x = 0} \\ x(x\text{ - 8) = 0} \\ x\text{ = 0 or x- 8 = 0} \\ \\ x\text{ - 8 = 0} \\ x\text{ = 8} \end{gathered}`

From our result, the dolphin is 8 ft from its starting point (option A)