1 Answer

Cfkane · Answer 1 · 2023-03-06T02:06:04+0000

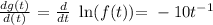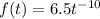
then we have a new function:

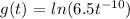
$g(t)\text{ = }ln(6.5t^(-10)\text{)}$

its derivative is: the derivative of the outer function (natural logarithm) times the derivative of the inner function 6.5t^-10

that is:

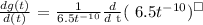
$(dg(t))/(d(t))\text{ = }(1)/(6.5t^(-10))\frac{d}{d\text{ t}}\text{( }6.5t^(-10))^(\square)$

the above because the derivative of the function ln is 1 / x , where in this case x = 6.5t^-10.

The above equation is equivalent to:

$(dg(t))/(d(t))\text{ = }(1)/(6.5t^(-10))\text{( -10 x}6.5t^(-11))^(\square)=\text{ }(1)/(6.5t^(-10))\text{( -}65t^(-11))=-10t^(-1)$

So the correct answer is:

$(dg(t))/(d(t))\text{ = }(d)/(dt)\text{ }\ln (f(t))\text{= }-10t^(-1)$

Please log in or register to add a comment.