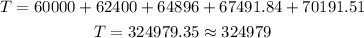Question

7. A company offers you a job with an annual salary of $60 000 for the first year and a 4% raise every year after. Approxin ately how much money in total would you earn in 5 years of working there? $324979$72999$312000$72000

Answer 1

Using the formula for the future value

`A=p\cdot(1+i)^t`

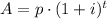
in which p is the annual salary for the first year, i the raise per year and t the time in years.

We calculate only 4 years with the increment because in the first year there is not a raise.

Replace in the formula

`\begin{gathered} A=60000\cdot(1+0.04)^4 \\ A=70191.51 \end{gathered}`

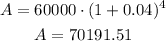
then calculate this for the other years and add all the future values together.

`\begin{gathered} A=60000\cdot(1+0.04)^4 \\ A=70191.51 \end{gathered}`
`\begin{gathered} A=60000\cdot(1+0.04)^3 \\ A=67491.84 \end{gathered}`
`\begin{gathered} A=60000\cdot(1+0.04)^2 \\ A=64896 \end{gathered}`
`\begin{gathered} A=60000\cdot(1+0.04) \\ A=62400 \end{gathered}`

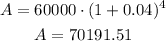
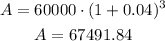
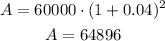
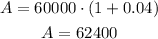
add all together

`\begin{gathered} T=60000+62400+64896+67491.84+70191.51 \\ T=324979.35\approx324979 \end{gathered}`