Question

Two objects are placed so their centers are 1.54 meters apart, and the force between them is 7.14 x 10-10 newtons. What is the mass of each object if one has twice the mass of the other?

Answer 1

Given:

The distance between the two objects is r = 1.54 m

The force between the two objects is

`F=\text{ 7.14}*10^(-10)\text{ N}`

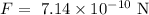
Let the mass of the object is m and the mass of the other object is 2m

To find the mass of each object.

Step-by-step explanation:

The mass can be calculated by the formula

`\begin{gathered} F=(Gm*(2m))/(r^2) \\ m=(Fr^2)/(2G) \end{gathered}`

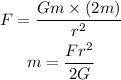
Here, G is the universal gravitational constant whose value is

`G\text{ = 6.67}*10^(-11)\text{ N m}^2\text{ /kg}^2`

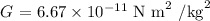
On substituting the values, the mass will be

`\begin{gathered} m=(7.14*10^(-10)*(1.54)^2)/(2*6.67*10^(-11)) \\ =12.69\text{ kg} \end{gathered}`

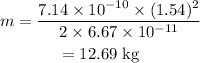
The mass of the other object will be

`2m\text{ = 25.38 kg}`

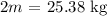
Final Answer:

The mass of the first object is 12.69 kg

The mass of the second object is 25.38 kg