The answer is very simple. .
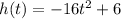
In this equation the heights values are substituted to determine the times.
For h = 2 feet
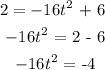
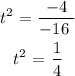
![t\text{ = }\sqrt[]{(1)/(4)}\text{ = }0.5\text{ seconds}](https://img.qammunity.org/2023/formulas/mathematics/college/c14slbcneozyx95luswsdj5cjym12dm6qv.png)
That would be the first time corresponding to the height of 2 feet.
We still need to calculate the time for the other height.
For h = 5 feet
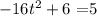
![\begin{gathered} -16t^2\text{ = 5 -6 } \\ -16t^2\text{ = -1} \\ t^2\text{ = }(1)/(16) \\ t\text{ = }\sqrt[]{(1)/(16)}\text{ = }0.25\text{ seconds} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6b3wepw2lfr76uuegjv5up4srjro9kh26l.png)
The answer is: Riley should try to catch the ball between 0.25 and 0.5 seconds.