The following equation describes the height h of the ball after an amount of time of t seconds.
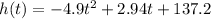
The ground represents the height zero, therefore, to find the corresponding time when the ball hits the ground we just have to solve the equation
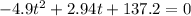
To solve this equation we can use the quadratic formula.
Our solutions are

Our solution is only the positive root.
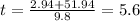
The object strikes the ground after 5.6 seconds.