Given:
The coordinates of line segment AB are given as follows:
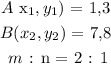
Required:
Coordinate of point which divides the given line segment in a ratio of 2:1.
Assume the required point as P(x,y).
Step-by-step explanation:
The required coordinate of point P is calculated using the section formula for internal division.
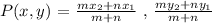
Substituting the values in the formula,
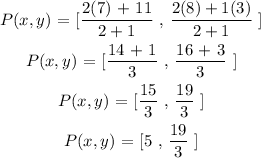
Answer:
Thus the coordinate of the point P(x,y) which divides the line segment Ab in a ration 2 : 1 is,
![P(x,y)=\text{ \lbrack 5 ,}(19)/(3)\operatorname{\rbrack}]()