Question

Use a geometric mean theorem or set up similar triangles to solve for the variable or find the indicated side length.All answers should be in simplified radical form:Please enter a square root as follows:2v2 as 2sqrt2 OR V2 as sqrt2

Answer 1

The figure for the triangle is,

Consider the triangle ABD and triangle ABC.

`\begin{gathered} \angle ABD\cong\angle ABC\text{ (Common angle)} \\ \angle BAC=\angle BDA\text{ (Each right angle)} \\ \Delta ABD\approx\Delta CBA\text{ (By AA similarity)} \end{gathered}`

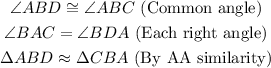
So triangle ABD is similar to triangle CBA. So ratio of sides of triangle are equal.

`(AD)/(AC)=(AB)/(CB)=(BD)/(AB)`

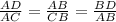
Determine the length of AB by using the ratio of sides.

`\begin{gathered} (AB)/(14)=(6)/(AB) \\ (AB)^2=84 \end{gathered}`

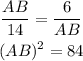
Consider the triangle ABD.

Determine the value of x by using the pythagoras theorem

`\begin{gathered} (AB)^2=x^2+(6)^2 \\ 84=x^2+36 \\ x=\sqrt[]{84-36} \\ =\sqrt[]{48} \\ =4\sqrt[]{3} \end{gathered}`

So value of x is,

`4\sqrt[]{3}`